ToT被华为诺亚方舟实验室升级了,Forest-of-Thought:让LLM多路径推理的Prompt框架
当前LLM推理能力的局限
大语言模型(LLM)在自然语言处理领域取得了巨大突破,但在复杂推理任务上仍面临着显著挑战。现有的Chain-of-Thought(CoT)和Tree-of-Thought(ToT)等方法虽然通过分解问题或结构化提示来增强推理能力,但它们通常只进行单次推理过程,无法修正错误的推理路径,这严重限制了推理的准确性。当遇到复杂的数学问题或逻辑推理任务时,这些方法往往会陷入局部最优解而无法自我纠正。
为了突破这一瓶颈,来自华为诺亚方舟实验室的研究团队提出了一个创新的推理框架 - Forest-of-Thought(FoT)。这个框架通过集成多棵推理树,引入稀疏激活和动态自我纠正机制,显著提升了LLM的推理能力。本文将深入解析FoT框架的工作原理、实现细节及其在实际应用中的表现。


LLM推理方法的演进
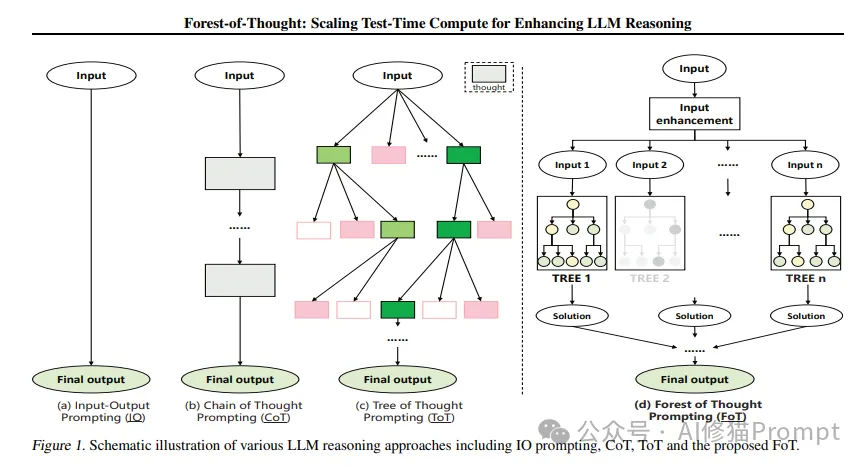
如图1所示,LLM推理方法经历了从简单到复杂的演进过程:
(a)IO Prompting:最基础的输入-输出模式,直接将问题输入获取答案,缺乏推理过程。
(b)Chain of Thought(CoT):引入了线性的思维链,通过步骤分解来增强推理能力。
(c)Tree of Thought(ToT):采用树状结构探索多个可能的推理路径。
(d)Forest of Thought(FoT):创新性地引入多棵推理树,并通过输入增强和稀疏激活来提升推理效果。
这种演进过程展示了LLM推理方法在复杂性和有效性上的不断提升。FoT通过集成多棵推理树,不仅扩展了推理空间,还通过树间的互补提高了推理的准确性。
Forest-of-Thought的核心思想
从单树到森林:多路径推理的优势
传统的Tree-of-Thought方法使用单棵决策树来模拟推理过程,每个节点代表一个决策点,边表示状态转换。这种方法的局限在于:一旦选择了错误的推理路径,就很难回溯和纠正。Forest-of-Thought突破性地提出了"思维森林"的概念,同时维护多棵推理树,每棵树从不同角度思考问题。这种多路径并行推理的方式不仅提高了找到正确解决方案的概率,还能通过树间的互补和验证来提升推理的可靠性。
稀疏激活:高效的推理路径选择
为了避免计算资源的浪费,FoT引入了稀疏激活策略。在推理过程中,只有最相关的推理树(或树中的特定节点)会被选择进行计算,而不是对所有树进行完整计算。具体来说,对于每棵推理树Ti,每一层只考虑得分最高的节点进行进一步推理。如果某一层的节点无法产生有效输出,该树的分裂过程将提前终止,激活指示值设为0;否则,树将继续分裂直到指定深度,激活指示值设为1。
动态自我纠正:提升推理准确性
FoT的另一个创新点是引入了动态自我纠正策略。对于每棵树的初始结果si,系统会评估其正确性和有效性,并在每个推理步骤完成时分配相应的分数。一旦某个步骤的分数低于预定阈值,就会自动触发纠正机制。这个机制首先回顾和分析过去的失败案例,识别低分的原因和常见错误模式,然后尝试纠正错误并优化推理方向。
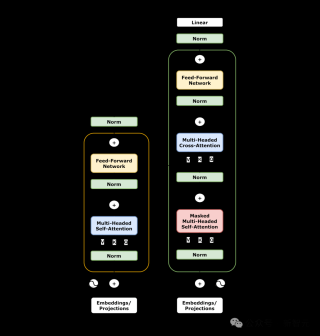
框架整体架构

FoT的算法实现如Algorithm 1所示,主要包含以下步骤:
- 初始化结果集S0
- 对n棵推理树进行迭代处理
- 每棵树Ti使用输入增强后进行推理
- 根据激活指示符ϕi决定是否进行动态自我纠正
- 更新结果集
- 最终通过CGED决策机制得出结果
这个算法流程体现了FoT框架的核心特点:多树并行推理、动态纠错和共识决策。
稀疏激活的实现方法
稀疏激活在树级别和节点级别都有实现。对于树Ti,其激活指示符ϕi定义为:
ϕi = { 1,如果树Ti被激活 0,如果树Ti未被激活 }
在节点级别,第l层节点k的激活由其得分si,l,k决定。只有得分位于该层前m的节点才会被激活:
Ai,l = {k | si,l,k 在第l层得分前m名内}
森林的最终输出综合考虑树级和节点级的激活:
y = Σ(i=1 to n) ϕi · [Σ(l=1 to Li) Σ(k∈Ai,l) fi,l,k(x)]
动态自我纠正机制
自我纠正机制包含以下步骤:
1.评分阶段:使用LLM对每个推理步骤进行评分 scorei ∼ pθ(scorei | si, x)
2.纠正阶段:当分数低于阈值时,基于历史失败案例C进行纠正 s'i ∼ pθ1(s'i | C, si, x)
3.数学规则匹配:对于数学任务,额外引入基于规则的快速纠正 s'i = F(si)
动态自我纠正机制的实现示例
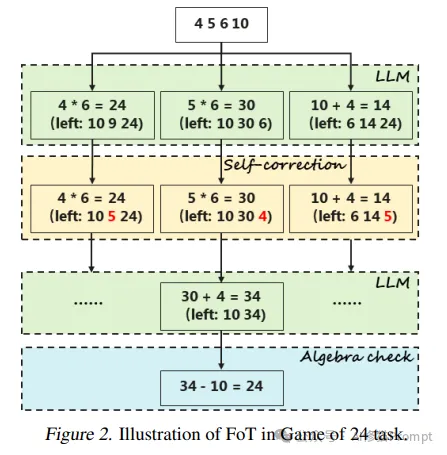
以24点游戏为例,图2展示了FoT如何通过多步骤推理和自我纠正来解决问题:
- LLM层:首先生成多个可能的计算步骤(4+6=24,5+6=30等)
- 自我纠正层:对初始结果进行评估和修正
- 再次使用LLM进行推理
- 最后通过代数检查验证结果
这个过程展示了FoT如何通过多层次的推理和纠错来提高解决问题的准确性。
实验验证与性能分析
实验设置
研究团队在三个广泛使用的LLM推理基准上评估了FoT方法:
- Game of 24
- GSM8K
- MATH
基础语言模型使用了Llama3-8B-Instruct,并在GSM8K基准上额外测试了Mistral-7B和GLM-4-9B。
实验结果分析
Game of 24任务
在24点游戏中,FoT展现出显著优势:
- 当树的数量从2增加到4时,准确率提升了14%
- 相比单纯增加叶节点数量,多树方法效果更好
- 在保持计算成本相近的情况下,FoT的准确率明显高于ToT
GSM8K基准测试
在GSM8K数据集上:
- 4-rollouts MCTSr配合2棵树的FoT比8-rollouts MCTSr提高了3.2%的准确率
- 随着树数量增加,多方法森林的优势更加明显
- 即使只使用2棵树的FoT,准确率提升也很显著
MATH基准测试
在MATH数据集的五个难度等级上:
- FoT(n=4)在Level-1到Level-5都显示出约10%的提升
- 性能提升在各个难度级别都保持稳定
- 证明了FoT在处理不同复杂度问题时的稳定性
实验结果分析
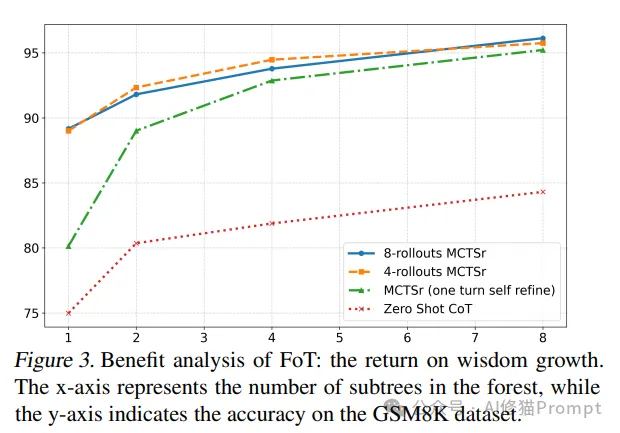
实验结果表明FoT在多个方面都优于传统方法:
1.基础方法对比:
- IO prompt和CoT prompt仅有3%的成功率
- 普通ToT(b=5)达到5.26%
- FoT(b=1,n=5)提升至9.47%
2.引入自我纠正后(*表示):
- 2棵树时达到77.89%
- 4棵树时达到91.58%
- 8棵树时达到96.84%
- 16棵树时实现100%的成功率
- ToT*的性能显著提升,从5.26%提升到56.25%-76.84%
- FoT*展现出更强的优势:
3.计算成本分析:
- FoT虽然需要更多推理次数,但通过稀疏激活策略控制了计算开销
- 性能提升远超计算成本的增加
实践启示与应用建议
对Prompt工程师的启示
1.多角度思考的重要性
- 在设计复杂推理任务的提示时,考虑引入多个推理路径
- 通过不同视角的提示来增强模型的推理能力
- 设计互补的提示策略以提高推理准确性
2.错误处理机制的设计
- 在提示中加入自我检查和纠错的机制
- 设计分阶段的推理过程,便于及时发现和纠正错误
- 利用历史经验来优化推理策略
3.计算资源的高效利用
- 采用分层的提示策略,避免资源浪费
- 根据任务复杂度动态调整推理深度
- 在保证准确性的前提下优化计算效率
实际应用场景
1.复杂数学问题求解
- 将问题分解为多个子问题
- 通过不同路径并行求解
- 综合多个解法得出最优答案
2.逻辑推理任务
- 设计多层次的推理框架
- 引入验证和纠错机制
- 通过多角度分析提高推理准确性
3.决策支持系统
- 构建多维度的决策树
- 实现动态调整和优化
- 提供可靠的决策建议
写在最后
Forest-of-Thought框架通过创新的多路径推理方法,成功突破了传统LLM推理的局限。其核心优势在于:
1.多维思维能力
- 通过多棵推理树实现多角度思考
- 提高问题解决的全面性和准确性
- 增强模型的推理鲁棒性
2.高效的资源利用
- 采用稀疏激活策略
- 优化计算资源分配
- 提高推理效率
3.可靠的纠错机制
- 实现动态自我纠正
- 学习历史经验
- 持续优化推理质量
这一框架为提升LLM的推理能力提供了新的思路和方法,对于开发更智能、更可靠的AI系统具有重要的指导意义。对于Prompt工程师而言,理解和运用FoT的核心理念,将有助于设计出更有效的提示策略,开发出更强大的AI应用。
文章来自于“AI修猫Prompt”,作者“AI修猫Prompt”。

























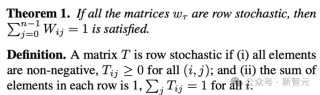
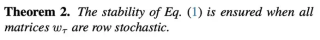










全部评论
留言在赶来的路上...
发表评论